Inhoud

• Stappen
• Tips

Wiskundigen en grafische programmeurs moeten vaak de hoek tussen twee vectoren vinden. Gelukkig vereist de formule die wordt gebruikt om deze hoek te berekenen niets meer dan een eenvoudig scalair product. Hoewel de redenering achter deze formule gemakkelijker te begrijpen is bij het gebruik van tweedimensionale vectoren, kunnen we deze gemakkelijk aanpassen aan vectoren met een willekeurig aantal componenten.

Stappen

Deel 1 van 2: Bereken de hoek tussen twee vectoren

1. 

   Identificeer de twee vectoren. Schrijf alle bekende informatie over de twee vectoren op. Voor deze tutorial gaan we ervan uit dat u de vectoren alleen kent in termen van hun dimensionale coördinaten (ook wel componenten). Als je het module of standaard- van deze vectoren (dat wil zeggen, hun lengte), kunt u enkele van de onderstaande stappen overslaan.
   • Voorbeeld: we kijken naar de tweedimensionale vectoren = (2,2) en = (0,3). Deze twee vectoren kunnen worden herschreven als = 2ik + 2j e = 0ik + 3j = 3j.
   • Hoewel ons voorbeeld twee tweedimensionale vectoren gebruikt, kunnen we de volgende instructies toepassen op vectoren met een willekeurig aantal componenten.

2. 

   
   
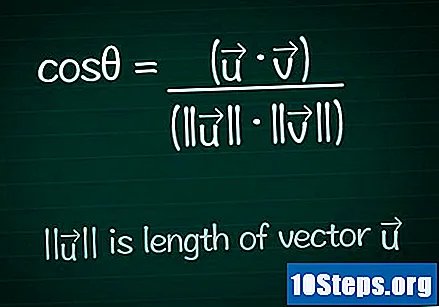
   Schrijf de cosinusformule. Om de waarde van de hoek θ tussen twee willekeurige vectoren te vinden, moeten we eerst de cosinus van die hoek berekenen. U kunt de formule in detail zoeken en uitzoeken, of gewoon schrijven zoals hieronder:
   • cosθ = (•) / (|||| ||||)
   • |||| vertegenwoordigt de module (of lengte) van de vector ".
   • • vertegenwoordigt de scalair product (of intern product) van de twee vectoren.

3. 

   
   
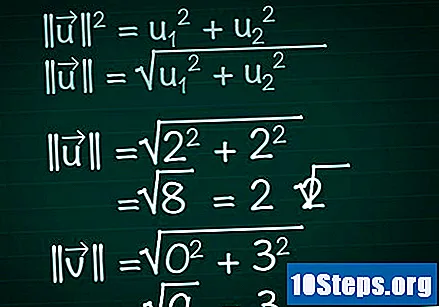
   Bereken de modulus van elke vector. Stel je een rechthoekige driehoek voor die wordt gevormd door het onderdeel X van een vector, zijn component y en de vector zelf. In deze driehoek speelt de vector de rol van de hypotenusa; daarom zullen we de stelling van Pythagoras toepassen om de lengte ervan te bepalen. Als resultaat is deze formule gemakkelijk toepasbaar op vectoren met een willekeurig aantal componenten.
   • || u || = u₁ + u₂. Als de vector meer dan twee componenten heeft, ga dan gewoon door met het toevoegen van + u₃ + u₄ +...
   • Daarom zullen we voor een tweedimensionale vector moeten || u || = √ (u₁ + u₂).
   • In ons voorbeeld |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   Bereken het scalaire product tussen de twee vectoren. Je zou de methode voor het vermenigvuldigen van vectoren al moeten kennen, ook wel scalair product. Om het scalaire product van twee vectoren in termen van hun componenten te berekenen, vermenigvuldigen we de componenten in dezelfde richting met elkaar en tellen we vervolgens de resultaten van die producten op.
   • Als u met grafische computerprogramma's werkt, bezoek dan eerst het gedeelte "Tips" voordat u verder gaat.
   • In wiskundige termen, • = u₁v₁ + u₂v₂, waarbij u = (u₁, u₂). Als uw vector meer dan twee componenten heeft, gaat u gewoon door met het toevoegen van + u₃v₃ + u₄v₄...
   • In ons voorbeeld • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dit is de waarde van het scalaire product tussen de vectoren en.

5. 

   Vervang deze resultaten in de cosinusformule. Onthoud, cosθ = (•) / (|||| || ||). We hebben het scalaire product en de module van de twee vectoren al berekend. Laten we nu deze waarden in de formule vervangen en de cosinus van de hoek berekenen.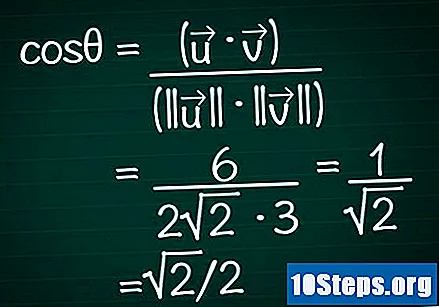
   • In ons voorbeeld cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Zoek de hoek op basis van je cosinus.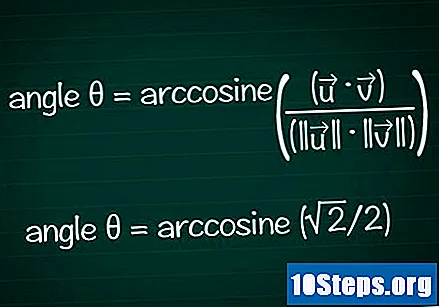
   Gebruik de boog- of cos-functie van uw rekenmachine om de hoek θ van uw cosinuswaarde te bepalen. In sommige gevallen kunt u de hoekwaarde wellicht vinden op basis van de eenheidscirkel.
   • In ons voorbeeld cosθ = √2 / 2. Typ "arccos (√2 ​​/ 2)" in je rekenmachine om de hoek te vinden. Een andere optie is om te zoeken naar de hoek θ van de eenheidscirkel waarbij cosθ = √2 / 2: dit geldt voor θ = /₄ of 45 °.
   • Als we alle informatie samenvoegen, hebben we de uiteindelijke formule θ = arccosine ((•) / (|||| || ||))

Deel 2 van 2: De formule definiëren voor het berekenen van de hoek

1. 

   Begrijp het doel van de formule. De formule die we gebruikten om de hoek tussen twee vectoren te berekenen, was niet afgeleid van reeds bestaande regels; in plaats daarvan is het gemaakt als een definitie van het scalaire product tussen twee vectoren en de hoek ertussen. Deze beslissing is echter niet willekeurig. Als we de basisgeometrie nader bekijken, kunnen we zien waarom deze formule resulteert in zulke nuttige en intuïtieve definities.
   • De volgende voorbeelden maken gebruik van tweedimensionale vectoren omdat ze het meest intuïtieve type zijn om mee te werken. De eigenschappen van vectoren van drie of meer dimensies zijn gedefinieerd op basis van de algemene formule (ook op een vergelijkbare manier).

2. 

   Bekijk de cosinuswet. Overweeg in elke driehoek de hoek θ gevormd door de zijkanten De en B en de zijkant ç tegenover die hoek. Volgens de cosinuswet is c = a + b -2abtailleband(θ). De demonstratie van deze formule kan gemakkelijk worden verkregen door kennis van de basisgeometrie.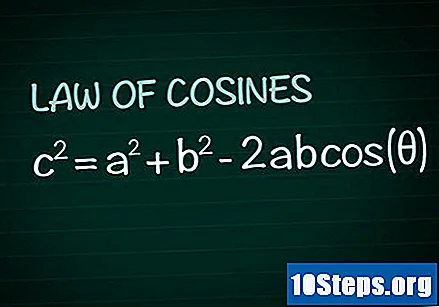

3. 

   Verbind de twee vectoren om een ​​driehoek te vormen. Teken een paar vectoren, en, met een hoek θ ertussen. Teken vervolgens een derde vector ertussen om een ​​driehoek te vormen. Met andere woorden, teken de vector zodanig dat + =, of gewoon = -.

4. 

   Pas de cosinuswet toe op deze driehoek. Vervang de lengte van de zijkanten van onze vector driehoek (dat wil zeggen, de vectormodule) in de formule voor de cosinuswet:
   • || (a - b) || = || een || + || b || - 2 || een || || b ||tailleband(θ)

5. 

   Herschrijf de formule met scalaire producten. Onthoud dat het puntproduct de vergroting is van een vector die op een andere wordt geprojecteerd. Het scalaire product van een vector zelf vereist geen projectie omdat er geen richtingsverandering is. Dit betekent dat • = || a ||. Laten we op basis van deze informatie de vergelijking van de cosinuswet herschrijven:
   • (-) • (-) = • + • - 2 || a || || b ||tailleband(θ)

6. 

   Vereenvoudig de formule. Vouw de producten aan de linkerkant van de vergelijking uit en vereenvoudig deze totdat je de formule bereikt die we kennen voor het berekenen van hoeken.
   • • - • - • + • = • + • - 2 || a || || b ||tailleband(θ)
   • - • - • = -2 || a || || b ||tailleband(θ)
   • -2 (•) = -2 || a || || b ||tailleband(θ)
   • • = || een || || b ||tailleband(θ)

Tips

• Voor een snelle oplossing past u de volgende formule toe op een tweedimensionaal vectorpaar: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Als u met grafische computerprogramma's werkt, hoeft u hoogstwaarschijnlijk alleen de richting van de vectoren te weten, niet hun lengte. Volg de onderstaande stappen om de vergelijkingen te vereenvoudigen en uw programma te versnellen:
  • Normaliseer elke vector, dat wil zeggen, zoek de eenheidsvector die dezelfde richting heeft als de originele vector. Om dit te doen, deelt u elke component van de vector door de vectormodule.
  • Bereken het scalaire product van de genormaliseerde vectoren, niet de originele vectoren.
  • Omdat de modulus (dat wil zeggen de lengte) van de genormaliseerde vectoren unitair is, kunnen we ze buiten de formule laten. Uw laatste vergelijking voor het berekenen van hoeken is bogen (•).
• Aan de hand van de formule van de cosinuswet kunnen we snel achterhalen of de betreffende hoek acuut of stomp is. Begin met cosθ = (•) / (|||| ||||):
  • De linker- en rechterkant van de vergelijking moeten hetzelfde teken hebben (positief of negatief).
  • Omdat de lengtes altijd positief zijn, zal cosθ altijd hetzelfde teken hebben als het scalaire product.
  • Daarom, als het scalaire product positief is, zal cosθ positief zijn. Dit betekent dat de hoek zich in het eerste kwadrant van de eenheidscirkel bevindt, dat wil zeggen θ <π / 2 of 90 °. Daarom is de hoek scherp.
  • Als het scalaire product negatief is, is cosθ negatief. Dit betekent dat de hoek zich in het tweede kwadrant van de eenheidscirkel bevindt, dat wil zeggen π / 2 <θ ≤ π of 90 ° <θ ≤ 180 °. Daarom is de hoek stomp.